Demystifying Karnaugh Maps: A Comprehensive Guide to Boolean Logic Simplification
Related Articles: Demystifying Karnaugh Maps: A Comprehensive Guide to Boolean Logic Simplification
Introduction
With great pleasure, we will explore the intriguing topic related to Demystifying Karnaugh Maps: A Comprehensive Guide to Boolean Logic Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Demystifying Karnaugh Maps: A Comprehensive Guide to Boolean Logic Simplification

The realm of digital circuits thrives on the intricate dance of logic gates, each performing a specific operation on binary inputs to produce a binary output. While this foundational concept is straightforward, the complexity arises when designing circuits with multiple inputs and outputs. Herein lies the power of Karnaugh maps (K-maps), a graphical tool that simplifies Boolean expressions, making circuit design more efficient and cost-effective.
Understanding the Essence of K-Maps
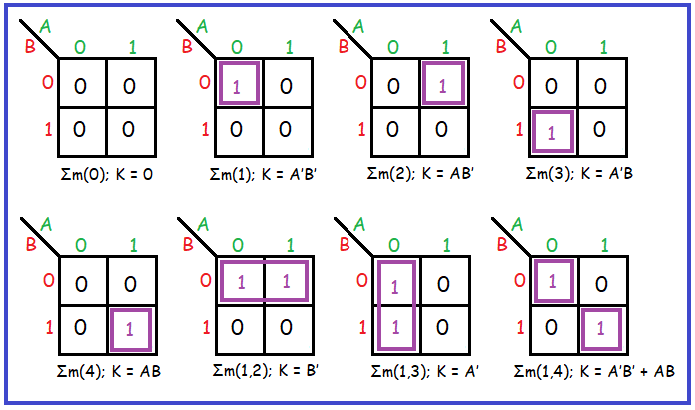
At its core, a K-map is a visual representation of a truth table, a tabular format that exhaustively lists all possible input combinations and their corresponding output values. However, unlike truth tables, K-maps strategically arrange these combinations in a grid, exploiting the inherent relationship between adjacent cells to facilitate simplification.
The grid’s structure is based on the number of input variables. Each row and column represents a unique combination of input values, with adjacent cells differing by only one variable. This arrangement ensures that adjacent cells with the same output value are physically close, enabling the identification of groups of cells that can be combined to simplify the Boolean expression.
The Art of Grouping: Unveiling Simplified Expressions
The key to K-map simplification lies in identifying and grouping adjacent cells with a value of ‘1’. These groups, referred to as ‘minterms’, represent logical terms in the Boolean expression. The simplification process hinges on the following principles:
- Adjacent Cells: Adjacent cells differ by only one variable. For example, in a 2-variable K-map, cells with input combinations (0,0) and (0,1) are adjacent.
- Grouping: Groups must be rectangular or square, with sides being powers of two (1, 2, 4, 8, etc.).
- Maximum Coverage: The aim is to form the largest possible groups, encompassing as many ‘1’ cells as possible.
- Overlap: Groups can overlap, but each ‘1’ cell should be included in at least one group.
Once these groups are identified, the corresponding Boolean expression is simplified by identifying the common variables within each group. For instance, a group encompassing cells (0,0), (0,1), (1,0), and (1,1) would represent the term ‘1’ since all variables change across the group.
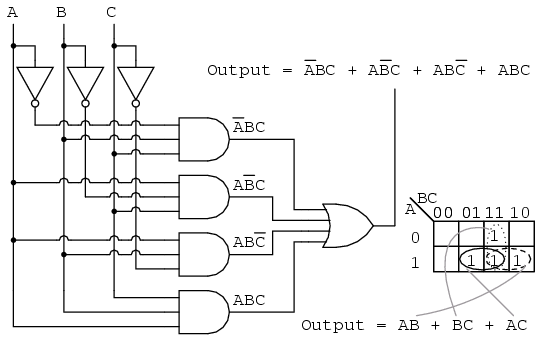
Illustrative Example: A 3-Variable K-Map
Consider a Boolean function with three input variables (A, B, C) and the following truth table:
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
To represent this function using a K-map, we create a 2×4 grid, with the rows representing the values of A and B, and the columns representing the values of C. The ‘1’ cells are placed according to the truth table, resulting in the following K-map:
C' C
AB 0 1
0 1 0
1 0 1By grouping the ‘1’ cells, we can identify the following minterms:
- Group 1: (A’B’C’) + (A’B’C) = A’B’
- Group 2: (A’BC’) + (A’BC) = A’B
- Group 3: (AB’C) + (ABC) = AC
The simplified Boolean expression for the function is therefore: A’B’ + A’B + AC.
Benefits of K-Maps
The use of K-maps offers numerous advantages in circuit design:
- Simplification: K-maps provide a systematic and intuitive method for simplifying complex Boolean expressions, leading to more efficient circuits.
- Reduced Complexity: By minimizing the number of terms and literals in the expression, K-maps reduce the number of logic gates required, resulting in simpler and more cost-effective circuits.
- Visual Aid: The graphical representation of K-maps makes it easier to visualize and understand the relationships between input variables and output values, aiding in the design process.
- Error Detection: K-maps help in identifying potential errors in the truth table or Boolean expression, leading to more accurate and reliable circuits.
FAQs: Addressing Common Queries
1. How do I determine the size of the K-map?
The size of a K-map is determined by the number of input variables. For ‘n’ input variables, the K-map will have 2^n cells. For example, a 4-variable K-map will have 2^4 = 16 cells.
2. What if there are multiple ‘1’ cells that cannot be grouped together?
If there are isolated ‘1’ cells that cannot be grouped with others, they are included as individual terms in the simplified expression.
3. What happens if there are multiple possible groupings?
In some cases, there may be multiple valid groupings that lead to different simplified expressions. The choice of grouping depends on the specific requirements of the circuit design.
4. Are K-maps limited to specific types of Boolean expressions?
K-maps can be used to simplify any Boolean expression, regardless of its complexity or the number of input variables.
5. Can K-maps be used for functions with multiple outputs?
Yes, K-maps can be used for functions with multiple outputs. A separate K-map is created for each output, and the simplification process is applied independently to each map.
Tips for Effective K-Map Usage
- Start Small: Begin by practicing with simpler K-maps before tackling more complex ones.
- Visualize: Use different colors or markers to highlight groups and simplify the process.
- Check for Errors: Carefully review the K-map and the simplified expression to ensure accuracy.
- Explore Alternatives: Consider different groupings and explore all possible simplifications.
- Experiment: Don’t be afraid to experiment and try different approaches to find the most efficient solution.
Conclusion: Embracing the Power of Simplification
Karnaugh maps are a powerful tool for simplifying Boolean expressions, making circuit design more efficient, cost-effective, and reliable. By understanding the principles of grouping and simplification, designers can leverage K-maps to create optimized circuits that meet specific performance requirements. The ability to visually represent and manipulate Boolean logic provides a powerful advantage, allowing for faster and more accurate circuit design. K-maps, therefore, are an indispensable tool for anyone working in the realm of digital circuits, facilitating the creation of sophisticated and efficient digital systems.






Closure
Thus, we hope this article has provided valuable insights into Demystifying Karnaugh Maps: A Comprehensive Guide to Boolean Logic Simplification. We thank you for taking the time to read this article. See you in our next article!