The Karnaugh Map: A Visual Tool for Simplifying Boolean Expressions
Related Articles: The Karnaugh Map: A Visual Tool for Simplifying Boolean Expressions
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to The Karnaugh Map: A Visual Tool for Simplifying Boolean Expressions. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
The Karnaugh Map: A Visual Tool for Simplifying Boolean Expressions

The realm of digital logic design hinges on the manipulation of Boolean expressions, which describe the relationships between binary inputs and outputs. Simplifying these expressions is crucial for creating efficient and cost-effective digital circuits. While algebraic methods exist, the Karnaugh map (K-map) offers a visual and intuitive approach to this simplification process.
Understanding the Essence of Karnaugh Maps
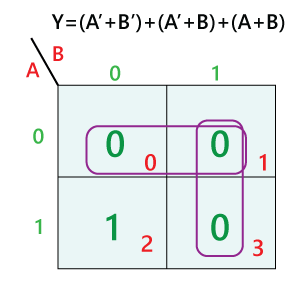
A Karnaugh map is a graphical representation of a Boolean function’s truth table. Each cell in the map corresponds to a unique combination of input variables, and the cell’s value (0 or 1) reflects the function’s output for that specific input combination. The map’s arrangement, however, is not arbitrary. It follows a specific pattern that allows for easy identification of adjacent cells representing minterms that differ by only one variable. This adjacency, coupled with the map’s structure, forms the foundation for simplification.
The Structure of a Karnaugh Map
The number of cells in a K-map is determined by the number of input variables. For a function with ‘n’ variables, the map will have 2^n cells. The cells are arranged in a grid, with each row and column representing a specific combination of input variables. The arrangement is designed such that adjacent cells differ in only one variable.
For instance, a two-variable K-map has four cells, arranged in a 2×2 grid. The rows and columns represent the two variables, with each cell representing a unique combination of these variables. A three-variable map has eight cells in a 2×4 grid, while a four-variable map has sixteen cells in a 4×4 grid.
Simplifying Boolean Expressions with Karnaugh Maps
The key to simplifying Boolean expressions using K-maps lies in identifying groups of adjacent cells with a value of ‘1’. These groups, called "prime implicants," represent terms in the simplified Boolean expression. The goal is to find the smallest number of prime implicants that cover all the ‘1’ cells in the map.
The Rules of Grouping
- Adjacency: Cells are considered adjacent if they differ in only one variable. This applies even to cells on the edges or corners of the map, as they are considered adjacent to their counterparts on the opposite side.
- Group Size: The size of a group must be a power of two (1, 2, 4, 8, etc.).
- Maximum Coverage: Each ‘1’ cell should be included in at least one group.
- Minimum Groups: The goal is to use the fewest possible groups to cover all the ‘1’ cells.
The Simplification Process
- Create the K-map: Construct the K-map based on the truth table of the function.
- Identify Prime Implicants: Circle groups of adjacent ‘1’ cells, following the grouping rules.
- Write the Simplified Expression: For each prime implicant, write the corresponding product term. The simplified expression is the sum of these product terms.
Benefits of Using Karnaugh Maps
- Visual Simplicity: K-maps offer a visual representation of Boolean functions, making it easier to grasp the relationships between input variables and outputs.
- Intuitive Simplification: The process of identifying prime implicants and grouping them is intuitive and visually appealing, aiding in the simplification process.
- Efficiency: K-maps can often lead to more simplified expressions compared to purely algebraic methods, especially for complex functions.
- Reduced Circuit Complexity: Simpler Boolean expressions translate to simpler and more efficient digital circuits, reducing component count and power consumption.
FAQs about Karnaugh Maps
Q: What are the limitations of K-maps?
A: K-maps are generally effective for functions with up to five or six variables. Beyond this, the map becomes too large and complex to be practical. Additionally, K-maps may not always provide the most optimal simplification in all cases.
Q: How do you handle "don’t care" conditions in K-maps?
A: "Don’t care" conditions represent input combinations where the output can be either ‘0’ or ‘1’. These conditions can be utilized to further simplify the expression by including them in groups of ‘1’ cells, effectively expanding the size of the groups.
Q: Can K-maps be used for functions with multiple outputs?
A: Yes, K-maps can be used for functions with multiple outputs. A separate map is constructed for each output, and the simplification process is applied independently.
Tips for Using Karnaugh Maps
- Start with a clear truth table: Ensure the truth table accurately represents the function before constructing the K-map.
- Pay attention to adjacency: Carefully identify all adjacent cells, including those on the edges and corners.
- Maximize group size: Aim for the largest possible groups to minimize the number of terms in the simplified expression.
- Use "don’t care" conditions strategically: Include "don’t care" conditions in groups to potentially achieve further simplification.
- Check for redundancies: After identifying prime implicants, ensure that there are no redundant terms in the simplified expression.
Conclusion
The Karnaugh map is a powerful tool for simplifying Boolean expressions, offering a visual and intuitive approach that complements traditional algebraic methods. Its ability to streamline the simplification process leads to more efficient digital circuits with reduced complexity and cost. While K-maps have limitations for functions with a large number of variables, their application remains valuable in numerous digital design scenarios. By understanding the principles of K-map construction and simplification, designers can effectively leverage this tool to create optimized and cost-effective digital circuits.





Closure
Thus, we hope this article has provided valuable insights into The Karnaugh Map: A Visual Tool for Simplifying Boolean Expressions. We thank you for taking the time to read this article. See you in our next article!

