The Power of Karnaugh Maps: A Comprehensive Exploration
Related Articles: The Power of Karnaugh Maps: A Comprehensive Exploration
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to The Power of Karnaugh Maps: A Comprehensive Exploration. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
The Power of Karnaugh Maps: A Comprehensive Exploration

The realm of digital circuit design is replete with tools and techniques aimed at simplifying complex logic expressions and optimizing circuit implementation. Among these, the Karnaugh Map, often referred to as K-map, stands out as a visually intuitive and powerful method for Boolean algebra simplification. This article delves into the intricacies of K-maps, elucidating their underlying principles, demonstrating their practical application, and highlighting their significance in the field of digital electronics.
Understanding the Essence of Karnaugh Maps
At its core, a K-map is a graphical representation of a truth table, enabling the simplification of Boolean expressions by visually identifying and grouping adjacent minterms (product terms) that share common variables. This grouping process, known as "combining terms," leverages the fundamental Boolean algebra laws of consensus and absorption to arrive at a minimized expression.
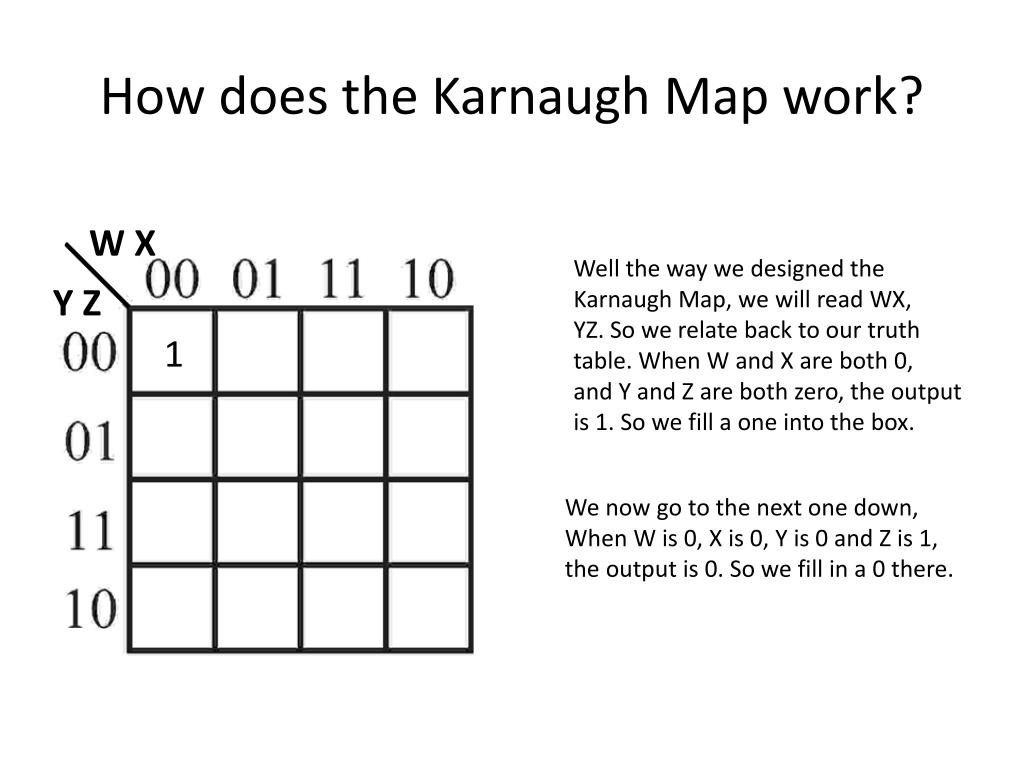
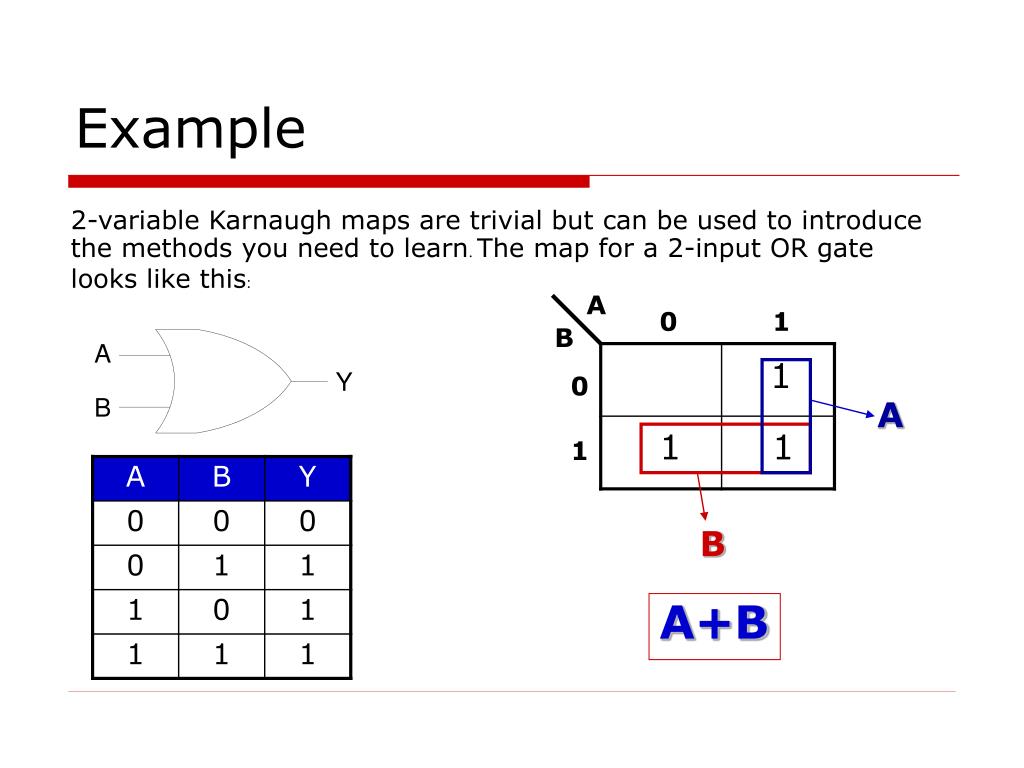
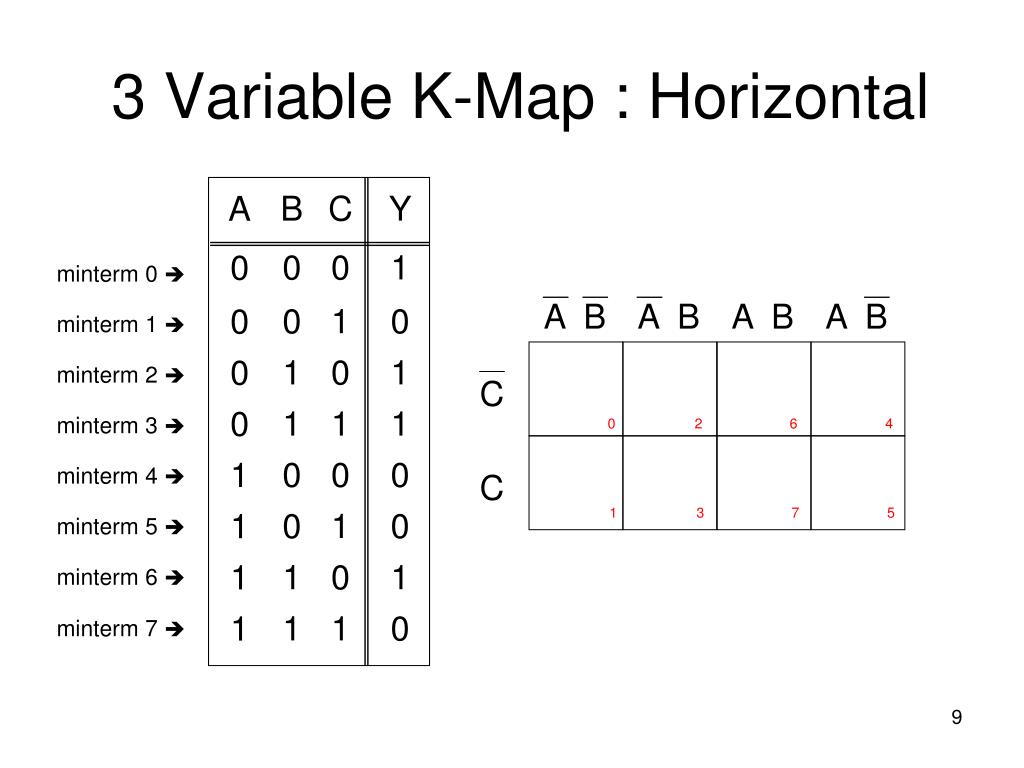
Constructing a Karnaugh Map
The construction of a K-map hinges on the number of input variables, with each cell representing a unique combination of input values. The arrangement of cells adheres to a specific pattern, ensuring that adjacent cells differ by only one variable. This strategic arrangement facilitates the identification of adjacent minterms for simplification.
The Process of Simplification
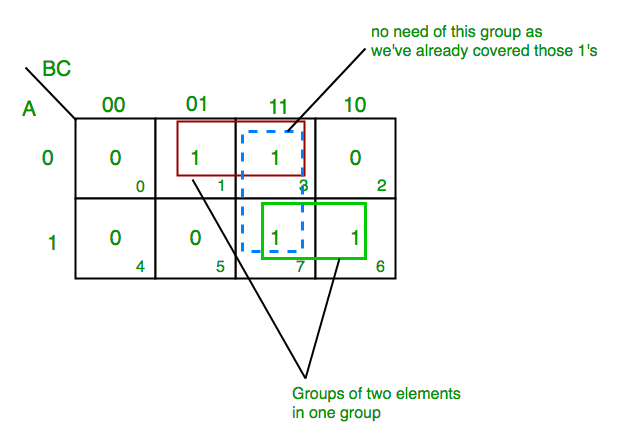
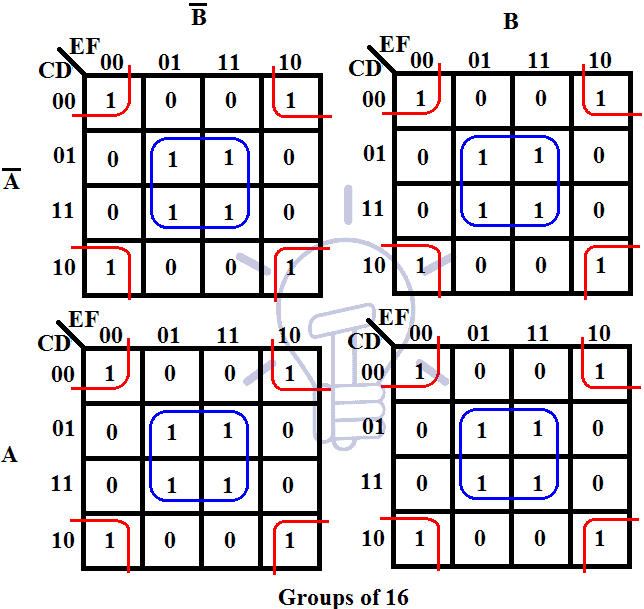
The simplification process involves identifying groups of adjacent "1" cells within the K-map. These groups can be of any size, as long as they are rectangular and contain a power of two cells (1, 2, 4, 8, etc.). Each group represents a simplified product term, with the variables common to all cells within the group included in the term.
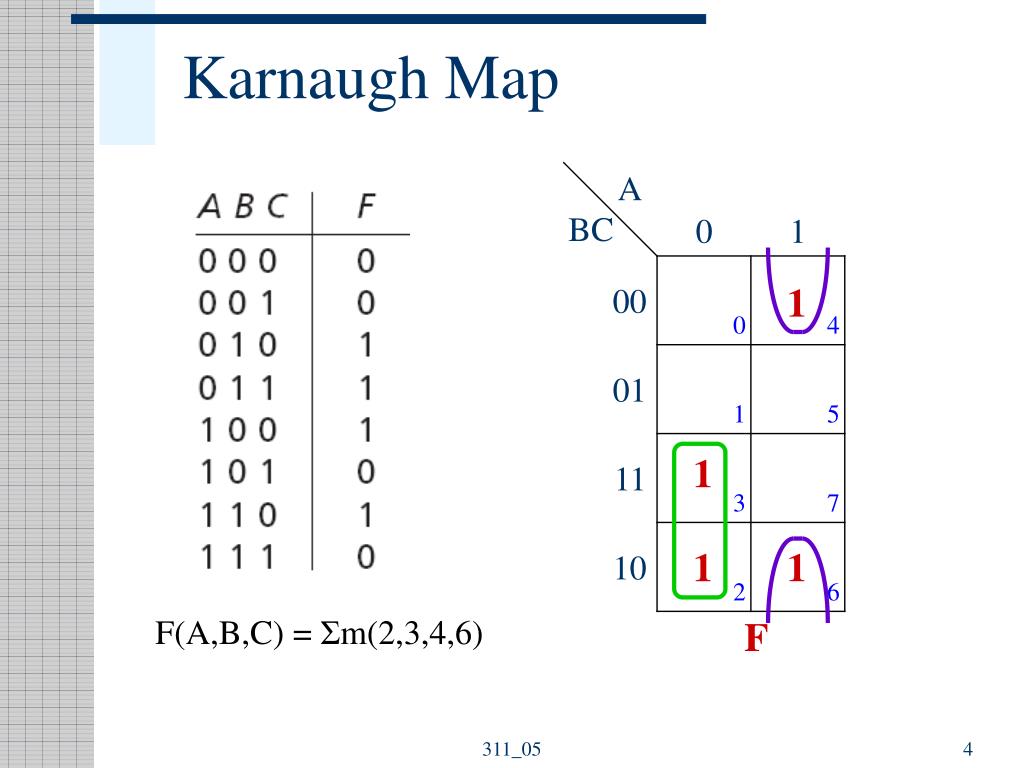
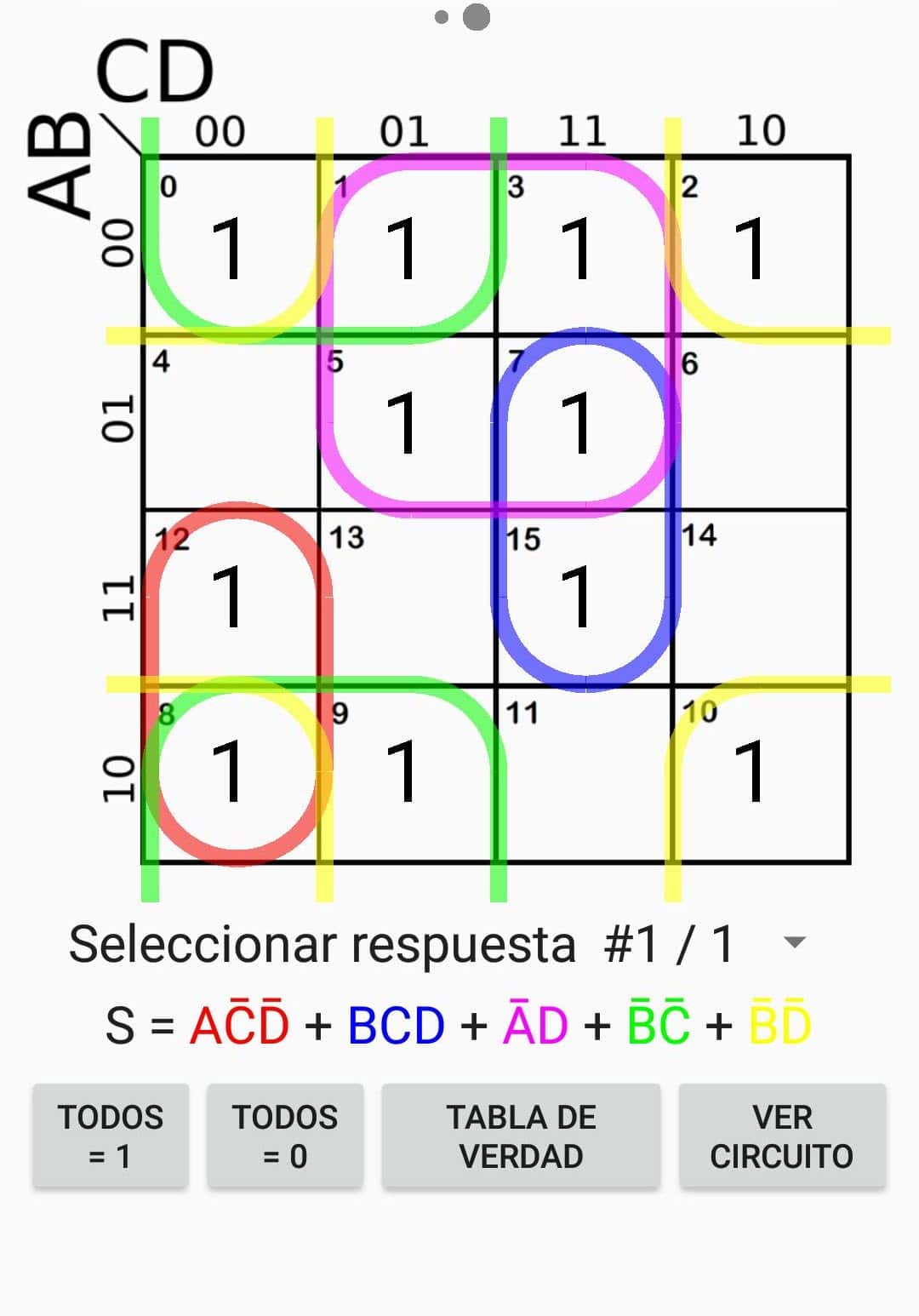
Illustrative Example
Consider a logic function with three input variables A, B, and C, represented by the following truth table:
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
The corresponding K-map would be constructed as follows:
AB
00 01 11 10
C 0 0 1 0 1
1 1 0 1 0By grouping the "1" cells, we obtain the following simplified expression:
Output = A’B’C + AB’C’ + ABC
Beyond Simplification: Applications of K-maps
The utility of K-maps extends beyond merely simplifying Boolean expressions. They play a crucial role in:
- Logic Circuit Design: K-maps streamline the process of designing and implementing logic circuits, facilitating the selection of optimal gates and minimizing the overall circuit complexity.
- Fault Detection and Diagnosis: K-maps aid in identifying potential faults within logic circuits, simplifying the troubleshooting process.
- Digital Design Optimization: By minimizing the number of logic gates and interconnections, K-maps contribute to the optimization of digital circuits for improved performance and reduced cost.
Frequently Asked Questions about K-maps
Q: What are the limitations of K-maps?
A: While highly effective for simplifying Boolean expressions with a limited number of variables, K-maps become cumbersome and impractical for functions with more than five or six input variables.
Q: How do I choose the optimal grouping in a K-map?
A: The goal is to create the fewest, largest possible groups, as this minimizes the number of terms in the simplified expression.
Q: Can K-maps be used for functions with more than four variables?
A: While directly representing functions with more than four variables becomes complex, techniques like "map folding" can extend the applicability of K-maps to higher-order functions.
Tips for Effective K-map Utilization
- Start with a clear truth table: Ensure the truth table accurately represents the desired logic function.
- Identify adjacent "1" cells: Carefully examine the K-map to find the largest possible groups of adjacent "1" cells.
- Don’t overlook "don’t care" conditions: These can be used to advantage by including them in groups to further simplify the expression.
- Check for completeness: Verify that all "1" cells are included in at least one group.
- Validate the simplified expression: Use a truth table or Boolean algebra to confirm the correctness of the minimized expression.
Conclusion
The Karnaugh map, with its intuitive graphical representation, provides a powerful and efficient method for simplifying Boolean expressions, optimizing logic circuit design, and enhancing overall digital circuit efficiency. Its ability to visually capture the relationships between input variables and output values, combined with its straightforward grouping mechanism, makes it a cornerstone tool in the arsenal of digital electronics professionals. While its limitations for higher-order functions exist, K-maps remain an indispensable asset for minimizing logic complexity and achieving optimal digital circuit performance.

Closure
Thus, we hope this article has provided valuable insights into The Power of Karnaugh Maps: A Comprehensive Exploration. We hope you find this article informative and beneficial. See you in our next article!