Unlocking Digital Design: A Comprehensive Guide to Karnaugh Maps
Related Articles: Unlocking Digital Design: A Comprehensive Guide to Karnaugh Maps
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unlocking Digital Design: A Comprehensive Guide to Karnaugh Maps. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
- 1 Related Articles: Unlocking Digital Design: A Comprehensive Guide to Karnaugh Maps
- 2 Introduction
- 3 Unlocking Digital Design: A Comprehensive Guide to Karnaugh Maps
- 3.1 Understanding the Fundamentals: Logic Gates and Boolean Algebra
- 3.2 Unveiling the Power of Karnaugh Maps
- 3.3 Beyond the Basics: Advanced Techniques and Applications
- 3.4 FAQs on Karnaugh Maps
- 3.5 Tips for Effective K-Map Usage
- 3.6 Conclusion: The Enduring Value of Karnaugh Maps
- 4 Closure
Unlocking Digital Design: A Comprehensive Guide to Karnaugh Maps

The realm of digital electronics thrives on the ability to manipulate and control information in its most fundamental form: binary data. This manipulation is achieved through intricate circuits composed of logic gates, each performing a specific logical operation on binary inputs. However, as circuits grow in complexity, designing them efficiently and effectively becomes a daunting task. Enter the Karnaugh map (K-map), a powerful tool that simplifies the design process by visually representing Boolean expressions and revealing optimal circuit implementations.
Understanding the Fundamentals: Logic Gates and Boolean Algebra
Before delving into the intricacies of K-maps, it is crucial to grasp the foundation upon which they operate: logic gates and Boolean algebra. Logic gates are the building blocks of digital circuits, each implementing a specific logical operation on binary inputs. The most common logic gates are:
- AND gate: Outputs a "1" only if all inputs are "1," otherwise, it outputs a "0."
- OR gate: Outputs a "1" if at least one input is "1," otherwise, it outputs a "0."
- NOT gate: Inverts the input, outputting a "1" if the input is "0" and vice versa.
- XOR gate: Outputs a "1" if the inputs are different, otherwise, it outputs a "0."
- NAND gate: Outputs a "0" only if all inputs are "1," otherwise, it outputs a "1."
- NOR gate: Outputs a "1" only if all inputs are "0," otherwise, it outputs a "0."
Boolean algebra provides a mathematical framework for representing and manipulating logical operations using variables and operators. Variables represent binary inputs (0 or 1), and operators correspond to the functions of logic gates. For example, the expression "A AND B" can be represented in Boolean algebra as "A · B."
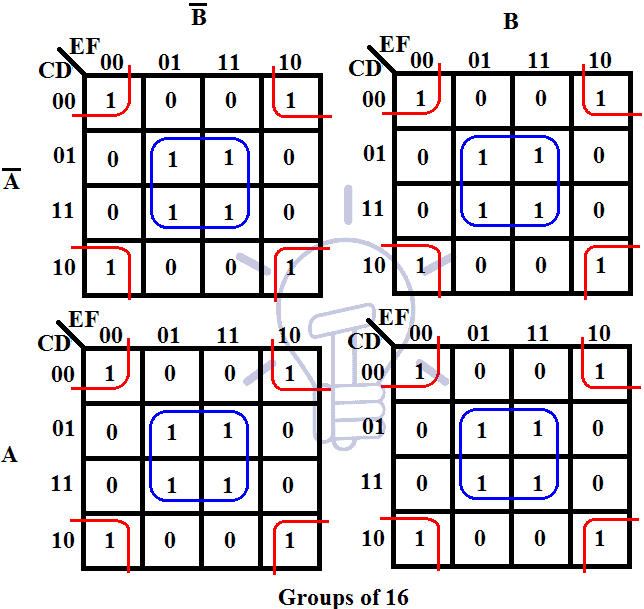
Unveiling the Power of Karnaugh Maps
A Karnaugh map is a graphical representation of a Boolean expression, designed to simplify the process of finding its minimal sum-of-products (SOP) or product-of-sums (POS) form. This simplification is crucial for achieving efficient circuit implementations, minimizing the number of logic gates required and reducing circuit complexity.
Key Features of K-maps:
- Grid structure: K-maps are structured as a grid where each cell represents a unique combination of input variables. The number of rows and columns in the grid depends on the number of input variables.
- Adjacent cells: Cells that share a single variable change (e.g., only one input variable flips from 0 to 1) are considered adjacent. This adjacency is crucial for identifying groups of "1"s, representing terms in the simplified Boolean expression.
- Gray code ordering: Input variables are arranged in a specific order known as Gray code, where only one bit changes between adjacent rows or columns. This ensures that adjacent cells in the map correspond to adjacent minterms in the truth table, facilitating the identification of groups.
Steps for Using K-maps:
- Construct the K-map: Create a grid with rows and columns corresponding to the input variables, arranged in Gray code order.
- Populate the K-map: Fill each cell of the map with the corresponding output value from the truth table or Boolean expression.
- Identify groups of "1"s: Circle groups of adjacent "1"s, ensuring that each group contains a power of 2 number of cells (1, 2, 4, 8, etc.). Larger groups are preferred as they represent simpler terms in the Boolean expression.
- Write the simplified expression: For each group, write the product of the input variables that are constant (unchanged) within the group. Combine these terms using OR operators to form the simplified SOP expression.
Example:
Consider a Boolean expression with three input variables (A, B, C) and the following truth table:
| A | B | C | Output |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
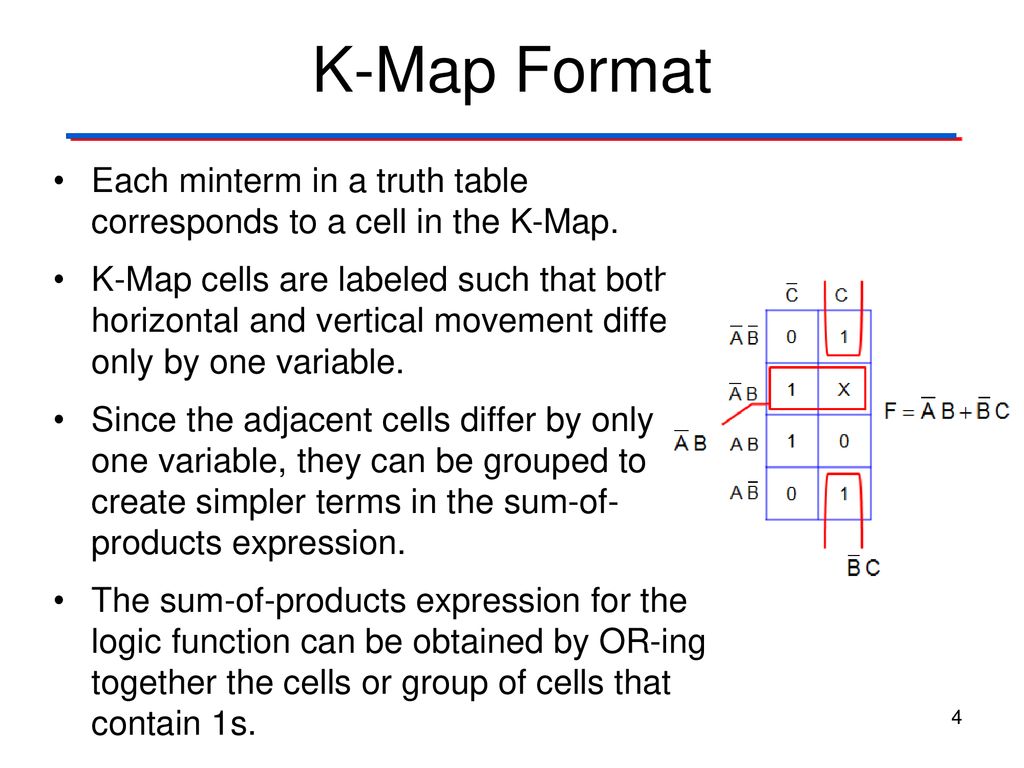
The corresponding K-map would be:
| C’B’ | C’B | CB | CB’ | |
|---|---|---|---|---|
| A’ | 0 | 1 | 0 | 1 |
| A | 1 | 0 | 1 | 0 |
Identifying the groups of "1"s and writing the simplified expression, we get:
- Group 1: A’B’C + A’BC’ + ABC = A’C’ + AC
- Group 2: AB’C’ + ABC = BC’
The simplified SOP expression is therefore: A’C’ + AC + BC’
Beyond the Basics: Advanced Techniques and Applications
While the basic principles of K-maps provide a powerful tool for circuit simplification, several advanced techniques and applications extend their utility even further:
1. Don’t Cares: In some cases, the output for certain input combinations may not be specified or irrelevant. These "don’t cares" can be strategically used to further simplify the Boolean expression by incorporating them into existing groups or creating new groups.
2. Product-of-Sums (POS) Simplification: K-maps can also be used to find the minimal POS form of a Boolean expression. This involves identifying groups of "0"s instead of "1"s and writing the sum of the input variables that are constant within each group.
3. Multiple Output Functions: K-maps can be used to simplify multiple output functions simultaneously. This is achieved by creating a separate K-map for each output function and then identifying common groups across the maps.
4. Multi-Level Logic Optimization: K-maps can be employed in multi-level logic optimization, where the circuit is decomposed into multiple levels of logic gates. This allows for further simplification and potential performance improvements.
5. Beyond Logic Design: K-maps find applications beyond digital circuit design. They can be used in areas like data analysis, image processing, and pattern recognition, where identifying patterns and simplifying complex relationships is crucial.
FAQs on Karnaugh Maps
1. How many variables can a K-map handle effectively?
While K-maps can be used for up to six variables, their effectiveness decreases beyond four or five variables. For larger numbers of variables, other simplification methods like Quine-McCluskey algorithm become more practical.
2. Can K-maps be used for functions with multiple outputs?
Yes, K-maps can be used to simplify multiple output functions simultaneously. Separate K-maps are created for each output, and common groups across the maps are identified to achieve further simplification.
3. How do "don’t cares" affect the simplification process?
"Don’t cares" can be strategically incorporated into existing groups or used to create new groups, further simplifying the Boolean expression. They provide flexibility in choosing the optimal simplification path.
4. What are the limitations of using K-maps?
K-maps become less efficient and cumbersome for functions with a large number of variables. Other methods, like the Quine-McCluskey algorithm, are more suitable for such cases.
5. Are there any software tools available for K-map simplification?
Yes, several software tools exist that can automatically generate and simplify K-maps. These tools can be helpful for complex designs and provide a visual representation of the simplification process.
Tips for Effective K-Map Usage
- Understand the Gray code ordering: Familiarize yourself with the Gray code arrangement of input variables to ensure accurate identification of adjacent cells.
- Start with smaller groups: Begin by identifying smaller groups of "1"s and gradually expand them into larger groups as possible.
- Utilize "don’t cares" strategically: Incorporate "don’t cares" to maximize simplification potential, but avoid creating groups solely based on "don’t cares."
- Verify the simplified expression: After obtaining the simplified expression, double-check its validity by comparing it to the original truth table or Boolean expression.
- Consider alternative simplification methods: For complex functions with many variables, explore other methods like the Quine-McCluskey algorithm for optimal simplification.
Conclusion: The Enduring Value of Karnaugh Maps
The Karnaugh map, despite its seemingly simple graphical representation, remains a cornerstone of digital circuit design. Its ability to visually simplify Boolean expressions and reveal optimal circuit implementations has made it an indispensable tool for engineers and designers across various fields. While other methods exist for circuit simplification, the K-map’s intuitive nature and visual representation continue to make it a valuable asset for understanding and manipulating logical functions, ensuring efficient and effective circuit design. As digital technology continues to evolve, the principles of K-maps will remain relevant, providing a foundation for tackling the complexities of modern digital design.





Closure
Thus, we hope this article has provided valuable insights into Unlocking Digital Design: A Comprehensive Guide to Karnaugh Maps. We hope you find this article informative and beneficial. See you in our next article!