Unlocking The Power Of Transformation: A Deep Dive Into Haskell’s Fmap

Unlocking the Power of Transformation: A Deep Dive into Haskell’s fmap

Related Articles: Unlocking the Power of Transformation: A Deep Dive into Haskell’s fmap

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unlocking the Power of Transformation: A Deep Dive into Haskell’s fmap. Let’s weave interesting information and offer fresh perspectives to the readers.

Unlocking the Power of Transformation: A Deep Dive into Haskell’s fmap

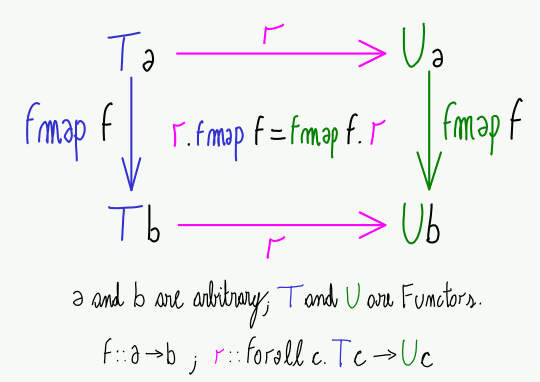
In the world of functional programming, Haskell stands out as a language that prioritizes the elegance and clarity of expressing computations. One of the key concepts that underpins this elegance is the concept of functors. While the term "functor" might sound intimidating, it represents a powerful abstraction that allows us to apply functions to values within data structures, seamlessly and consistently. The function fmap, often referred to as "map" in other languages, is the embodiment of this abstraction in Haskell, providing a powerful tool for transforming data while maintaining the structure of the original data container.

Understanding the Essence of Functors

Imagine a container holding a value. This container could be a list, a tree, or even a simple Maybe type. Now, imagine you want to apply a function to the value inside the container without altering the container itself. This is where the concept of a functor comes into play. A functor is a type that satisfies two laws:

1. Identity Law: Applying the identity function to a functor should have no effect.
2. Composition Law: Applying a function followed by another function to a functor should be equivalent to applying the composition of the two functions.

These laws ensure that functors behave consistently and predictably, allowing us to reason about their behavior with confidence.

fmap: The Workhorse of Transformation

fmap is a function that takes two arguments: a function (f) and a functor (x). It applies the function f to the value inside the functor x, returning a new functor with the transformed value. This might sound abstract, but let’s illustrate it with examples.

Example 1: Transforming Values in a List

fmap (+1) [1, 2, 3] -- Output: [2, 3, 4]

In this example, fmap takes the function (+1) and the list [1, 2, 3]. It applies the function (+1) to each element of the list, resulting in a new list [2, 3, 4] where each element has been incremented by one.

Example 2: Transforming Values in a Maybe

fmap (*2) (Just 5) -- Output: Just 10
fmap (*2) Nothing -- Output: Nothing

Here, fmap operates on a Maybe type. It applies the function (*2) to the value inside the Just constructor, doubling the value. In the case of Nothing, fmap preserves the Nothing structure, as there is no value to transform.

Benefits of Using fmap

The use of fmap brings numerous benefits to Haskell programming:

• Readability and Conciseness: fmap allows for a clear and concise way to express data transformations. The code becomes more readable and easier to understand, especially when dealing with nested structures.
• Code Reusability: fmap is a generic function that can be applied to various data structures, promoting code reuse and reducing redundancy.
• Type Safety: Haskell’s strong type system ensures that fmap will only apply functions to values that are compatible with the underlying functor type. This prevents runtime errors and helps to ensure the correctness of code.
• Compositionality: fmap allows for the composition of functions, enabling complex transformations to be built from simpler ones. This promotes modularity and code organization.

Beyond the Basics: Exploring fmap’s Applications

The power of fmap extends far beyond simple transformations. It plays a crucial role in various programming paradigms and techniques:

• Functional Programming: fmap is a cornerstone of functional programming, enabling the transformation of data without side effects. This promotes code purity and simplifies reasoning about program behavior.
• Data Structures: fmap is widely used for manipulating data structures like lists, trees, and maps. It provides a consistent way to apply transformations to the values within these structures.
• Error Handling: fmap can be used to propagate errors through computations. By applying functions to the Maybe type, we can handle errors gracefully and avoid unnecessary code duplication.
• Parallelism: fmap can be used to parallelize computations by applying functions to elements of a data structure in parallel. This can significantly improve performance for certain tasks.

FAQs about fmap

1. What is the difference between fmap and map?

While fmap is a generic function that works on any functor, map is a specific function designed for lists. In essence, map is a specialized instance of fmap for the list data structure.

2. Can I define my own functor?

Yes, you can define your own functor by defining a type and implementing the fmap function for that type. This allows you to extend the power of fmap to custom data structures.

3. How does fmap interact with other functions?

fmap can be combined with other functions like filter and foldr to perform more complex data manipulations. For example, you can use fmap to transform elements within a list before filtering them based on a certain condition.

4. Are there any limitations to using fmap?

While fmap is a powerful tool, it has limitations. For example, it cannot be used to modify the structure of the functor itself. If you need to change the structure of the data, you need to use other functions specific to the data structure you’re working with.

Tips for Effective Use of fmap

• Prioritize Clarity: Use fmap when the transformation is clear and concise. Avoid using it for overly complex or obscure transformations.
• Embrace Composition: Compose fmap with other functions to create powerful and expressive transformations.
• Understand Type Signatures: Pay close attention to the type signatures of fmap and the functions you are applying to ensure type compatibility.
• Explore Functors: Investigate different functor instances and experiment with their application in your code.

Conclusion

fmap is a fundamental concept in Haskell, providing a powerful and elegant way to transform data within functors. Its ability to apply functions consistently across various data structures, combined with its clear syntax and type safety, makes it an essential tool for any Haskell programmer. By understanding and utilizing fmap, you can write more concise, reusable, and maintainable code, unlocking the full potential of Haskell’s functional programming paradigm.

Closure

Thus, we hope this article has provided valuable insights into Unlocking the Power of Transformation: A Deep Dive into Haskell’s fmap. We appreciate your attention to our article. See you in our next article!